Another nostalgia+practice project I’m poking at on the Atari 800 XL is a Mandelbrot fractal generator, which I’m still in early stages of work on. This is mostly an exercise in building a 16-bit integer multiplier for the MOS 6502 processor, which has only addition, subtraction, and bit-shift operations.
The Mandelbrot set consists of those complex-plane points which, when iterating over z_i+1 = z_i^2 + c (where c is the input coordinate and z_0 = 0) never escape beyond |z_i| > 2. Surprisingly this creates a really cool shape, which has been the subject of fascination for decades:
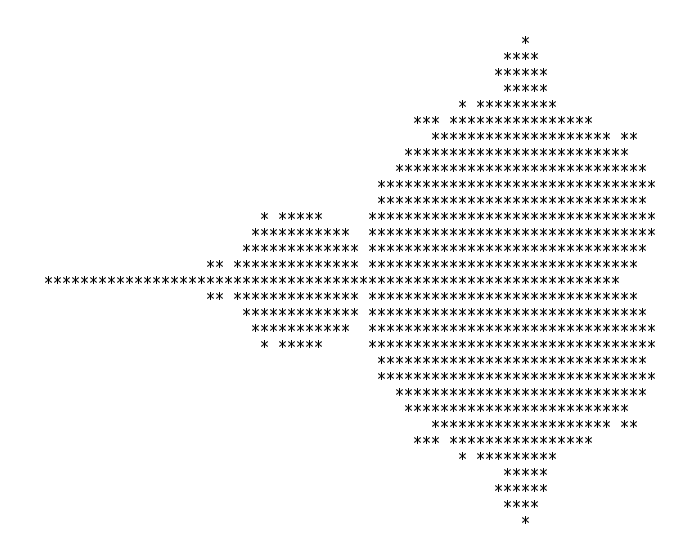
To implement this requires three multiplications per iteration, to calculate zx^2, zy^2, and zy*zx. Famous PC fractal program Fractint used for low zooms a 16-bit integer size, which is good because anything bigger gets real slow!
For higher zooms Fractint used a 32-bit integer and 29 fractional bits for Mandelbrot and Julia sets, which leaves a range from -4..3.9, plenty big enough. For the smaller 16 bit size that means 3.13 layout, should be plenty for a few zooms in on a 160×192 screen. :D Multiplication creates a 32-bit integer with twice the integer bits, so 6.26 with a larger range which covers the addition results for the new zx and zy values.
These then need to be shifted back up and multiplied to get zx^2, zy^2, and zy*zx for the next iteration; the boundary condition is zx^2 + zy^2 >= 4.
imul16
Integer multiplication when you have binary shifts and addition only is kinda slow and super annoying. Because you have to do several operations for each bit, every cycle adds up — a single 16-bit add is just 18 cycles while a multiply can run several *hundred* cycles, and varies based on input.
Note that a 650-cycle function means a runtime of about a half a millisecond on average (1.79 MHz processor, with about 30% of cycles taken by the display DMA). The whole shebang could easily take 2-3 ms per iteration with three multiplications and a number of additions and shifts.
Basically, for each bit in one operand, you either add, or don’t add, the other operand with the corresponding bitshift to the result. If you’re dealing with signed integers you need to either sign-extend the operands to 32 bits or negate the inputs and keep track of whether you need to negate the output; not extending can be faster because you can assume the top 16 bits are 0 and shortcut some operations. ;)
Status and next steps
imul16 seems to be working, though could maybe use more tuning. I’ve sketched out the mandelbrot iteration function but haven’t written it yet.
Another trick Fractint used was trying to avoid having to go to max iterations within the “Mandelbrot lake” by adding a check for periodic repetition; apparently when working with finite precision often you end up with the operations converging on a repeating sequence of zx & zy values that end up yielding themselves after one or a few iterations; these will never escape the boundary condition, so it’s safe to cut off without going to max iterations. I’ll have to write something up with a little buffer of saved values, perhaps only activated by an adjacent max-iters pixel.
Once the internals are working I’ll wrap a front-end on it: 4-color graphics display, and allow a point-n-zoom with arrow keys or maybe joystick. :D